昭和４９年度公立高校 入学選抜学力検査
数学
問一 次の計算をして、できるだけ簡単にせよ。
（ア） ６＋７×（−８）
（イ） 
（ウ） 
（エ） 
（オ） 
問二 全体集合をＮ＝
とし、Ａ，Ｂ，Ｐ，ＱをＮの部分集合とする。
次の集合を、要素（元）を書きならべる方法で表わせ。
（ア） Ａ＝
（イ） Ｂ＝
（ウ） Ｐ＝
Ｑ＝
のとき、Ｐ
Ｑ
問三 次の各問いに答えよ。
（ア） 男子２６人、女子１９人からなるクラスで、数学のテストの平均点は男子a点、女子ｂ点であった。このとき、クラスの平均点はいくらか。
（イ） 大、中、小の３個のサイコロを同時に投げるとき、出る目の数の和が５以下になる場合は何通りあるか。
（ウ） 下の表は、６人の生徒のあるテストの成績である。得点の標準偏差はいくらか。
|
生 徒 |
Ａ |
Ｂ |
Ｃ |
Ｄ |
Ｅ |
Ｆ |
平均点 |
|
得 点 |
６８ |
７０ |
６７ |
７６ |
７８ |
７１ |
７０ |
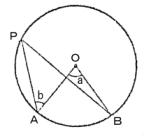問四 右の図の円Oについて、次の問に答えよ。
(ア)
，
の大きさを、それぞれ ａ, b とするとき、
の大きさをａ, bを用いた式で表わせ。
(イ)
円Oの半径が１２ｃｍ、
＝７５°のとき、弧AB（点Pをふくまない弧）の長さを求めよ。ただし、円周率は
として計算せよ。
問五 定義域が
である関数ｙ＝−x2 について、次の問に答えよ。
(ア) この関数の値域を、集合の記号を用いて表わせ。
(イ) ｘが２から４まで増加するとき、ｘの変化量に対するｙの変化量の割合を求めよ。
問六 右の図において、２点A，Bの座標をそれぞれ（３，３），（０，−１）とするとき、次の問に答えよ。
(ア) ２点Ａ，Ｂ間の距離を求めよ。
(イ) Aを中心とし、ＡＢを半径とする円はｘ軸と２点で交わる。この２点のｘ座標を求めよ。
(ウ) 直線ＡＢの上方の部分（原点０をふくむ側で、直線ＡＢはふくまない）は、どんな不等式の解の集合を表わすか、その不等式を求めよ。
問七 図のように、
が直角である直角二等辺三角形ＡＢＣの外接円の弧ＡＣ上に点Dをとり、ＢＤとＡＣの交点をＥとし、ＢＡとＣＤとの延長の交点をＦとして、次の問に答えよ。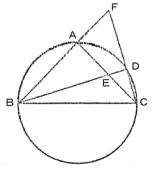
(ア) ＡＥ＝ＡＦであることを証明せよ。
(イ) ＥがＡＣの中点であるとき、△ABEと△DCEの面積の比を求めよ。
【昭和４９年２月２８日付 神奈川新聞より】